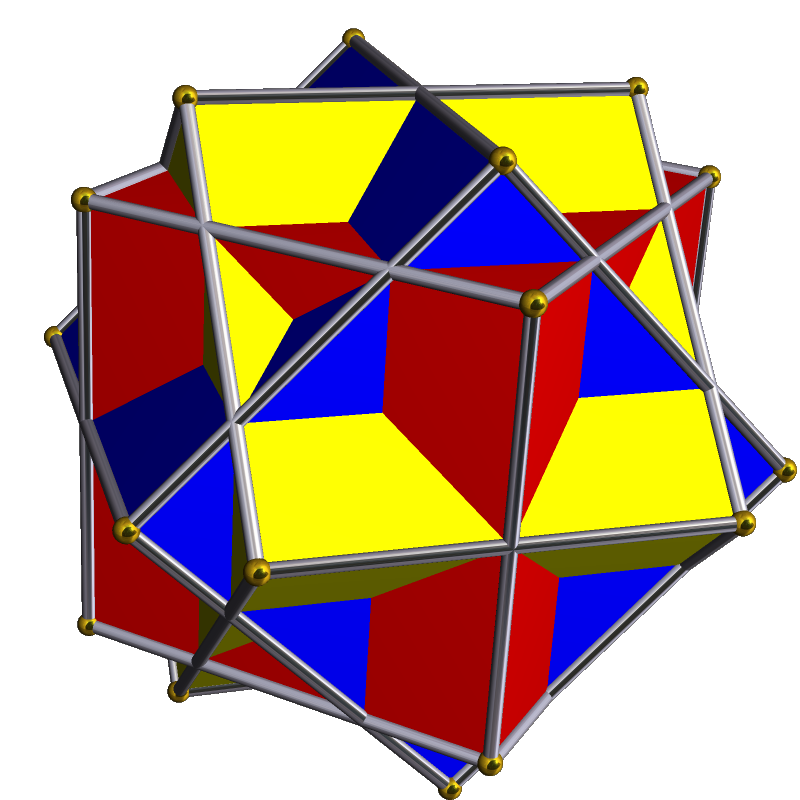
By The original uploader was Tomruen at English Wikipedia. - Transferred from en.wikipedia to Commons., CC BY-SA 3.0, Link
I learned about a year ago that the figure has been used in some discussion by a mathematician named John Skilling. I keep looking at it and thinking I get it, then it slips away. Unsurprisingly, MC Escher used it in a drawing, because of course he did. It is the most notoriously difficult problem on the Mega Test, which used to be used by the ultra-high IQ societies to sort amongst the highest scorers. I used to correspond with test designer Ron Hoeflin, who describes himself as a Schizoid Personality Disorder, and I believe it. Even among the highest scorers on the Mega, those who got over 45 out of 48 or better, less than a third got this one right. As I had already taken the test years ago and am not allowed a retake, I didn't think it would be cheating to scour the web to see if I could suss out the answer. The most common answer is 72 discrete spaces, which seems logical: 24 corners each intercepted by two planes, 24 x 3 = 72. Apparently that is wrong. The answer is greater than 68, however, because some determined SOB built one of these suckers out of rods and colored cellophane and then counted and got to 68 definite and answered that. He wondered if he might have missed at least one. Apparently even when you've got a hard model it's had to keep track. He concluded he got it wrong from his returned grade and the subsequent discussion by email among people who had qualified for the highest society. He now thinks the answer must be 69. Ron's not telling. One of the very few people who have gotten a 47 or the person who got a 48 must also know.
This was part of my eventually learning that I am not exceptional in my spatial intelligence, though it took me a long time to learn and admit that.
25 comments:
Havamal stanzas 54-6 treat the desirability of being middle-wise, not over-wise.
It seems to me that the consensus answer is 67. Ronald Penner writes about the problem here, and gives a heuristic argument not only for this compound, but also for the general case of n interpenetrating cubes: https://megasociety.org/noesis/133.pdf
Two instances of this figure are visible in "Waterfall" by M.C. Escher.
Ganzir
Thank you.
My earlier comment contained a mistake. Only one of the two figures on towers in "Waterfall" is a compound of three cubes, while the other, on the right tower from the viewer's perspective, is a compound of three octahedra.
Personally, I lack the spatial ability to determine by visualization how many subvolumes the three-cubes figure contains, and I have not found any detailed visual breakdown of why this compound contains 67 volumes, but multiple sources give 67 as the answer. Still, there is no proof that this or any other answer is correct.
Ganzir
Reading the Noesis pdf and DDGo-ing on a few related conversations, I think we can say that the formula is a reasonable conjecture. That's way more than I had before, so I'm good with that. When I time travel to the 1980s and take the test again, 67 will be my go-to answer. I have a couple of other Mega Test answers I think I could improve, but I don't think it will get me to Mega Society. I qualified for Prometheus and was president for a few years. I might have made Titan before it folded. You might hit my search bar for what I wrote about Grady Towers, Chris Langan, and Prometheus. I also had a series of essays about Billy Sidis that might be of interest, including the argument one of my readers had with my declaration that he was very smart but not of astronomical IQ.
I was born in 1999, long after the Mega and even Titan tests were released, and I think Ron stopped scoring the Mega when I was a toddler. I could still take the Power and Ultra tests, but would rather not pay $50 and wait around a month for a score report since I know I won't qualify for Mega with either, although the problems themselves are interesting.
Based on numerous tests, some of more questionable quality than others, my I.Q seems to be around 150, with a bias towards verbal and against spatial. Still, I could probably qualify for Prometheus, not to mention Mega, if I could travel back in time and submit answers easily discoverable on search engines today.
I scored 25 (19 verbal, 6 non-verbal) on Brainbreaker, the 'parallel form' of the Mega Test up to an isomorphism, which is available online at the links below. Making the reasonable assumption that a raw score of X on Brainbreaker equates to about the same I.Q. as does a raw score of X on Mega, that should theoretically qualify me at the Triple Nine level. I probably could have solved more with greater motivation, like the prospect of actually qualifying for a high-I.Q. society, but almost certainly without reaching the Prometheus bound (har har har).
https://alliqtests.com/tests/9/23/
https://alliqtests.com/tests/6/24/
I will look for your articles about Towers, Langan, Sidis, and Prometheus; thanks for the suggestions.
Ganzir
Great to hear from you, really. Spatial is also my weakest.
I belonged to both Triple Nine and ISPE back in the 80s. I sometimes think that I had just a bit of luck on what questions were asked and my Mega Test was a bit high. I now estimate my IQ as more like 150 than 164.
I have also discussed the limits of IQ tests here many times. I push back against the folks who say that we can't really define intelligence and the tests don't measure it, because the evidence is strong. I think they have a different objection which they are not articulating very well, that intelligence is not the most important quality for a human being to have, but we overvalue it. That's a more reasonable take. Even at the level of doing a job, most human endeavors require some other quality more than IQ, and even those that require a fair bit of IQ also require at least a couple of other qualities as well. Most tasks have a floor IQ to be able to accomplish it at all. But beyond that, a host of other things might be more important: charm, honesty, discretion, emotional control, determination, patience, or a hundred others.
Hopefully browsing around here will be entertaining. You are younger than all five of my sons, most of my nieces and nephews and even creeping into grandchild territory, so I am well-disposed toward hearing your thinking at all amidst all the old people who are the usual denizens here.
Thank you for the warm welcome!
Yes, I.Q. does not account for all interindividual variances in important behavioral phenotypes and social outcomes, and since any intelligence test is an imperfect measurement, I.Q. tests will be slightly more limited still. Nonetheless, it is about as manifest as anything can be that humans have a general aptitude for understanding, and that this facility differs tremendously between individuals. Whoever denies this can never be convinced otherwise, and can be safely assumed to either to be themselves deficient in the aptitude, or to be laboring under an ideological aversion to the idea of meaningful differences between people. Psychometrics only expounds on this obvious reality by naming its components, and by studying its biological underpinnings and correlations with other measurable variables. I question to what extent I.Q. tests are necessary, as a person's level of g is usually reflected in almost everything they do, and insofar as it is not, its importance is too tenuous to be concerned about anyway.
If you are interested, I have answers to all questions in the verbal sections of the Mega and Titan tests, although there may be a few mistakes. I received several answers from someone with an extremely high score on those sections combined; I think 45 or 46 out of 48. I also have answers to many, but far from all, of the non-verbal problems on those tests. I would prefer not to post them publicly, but I can e-mail them to you if you like.
Absolutely. Even though I would have to hunt down the original questions now. I think I got about a 37, my wife got about a 23.
email is wymanhome-at-comcast-dot-net
Oh, incidentally, Ron's answer for the five interpenetrating spheres question is 29. I know this because there was a website where you could take the test and have it scored against the official answer key. The site is down now, though. Also, I suspect that the answer Hoeflin accepts as correct hasn't been proven optimal. The same applies to some or maybe all of the 'maximum volumes' problems on his Titan Test.
Thanks
I now have the full answer key for the Mega Test Two. Are you interested in seeing it? If so, I can e-mail it to you, but I'll use a different e-mail address because I didn't renew the domain associated with the one I used last time.
Absolutely. Very grateful. wymanhome at comcast, etc.
I searched your blog for Chris Langan and didn't find anything
It was on quora, now that I think of it. I don't go there anymore, but i used to answer a lot of the IQ and mental health questions
About the three-interpenetrating-cubes problem, and several of the spatial problems on the Titan Test, all I can conclude is Psalms 139:6. I'm in one of the same I.Q. societies as Rick Rosner, although he doesn't actively participate in it as far as I know. Maybe I could coax him into showing me his answers.
Hehehe. This is reminiscent of James Bellinger's attitude over at "I Don't Know, But..." He is in my sidebarr. He just retired from being a physics prof at U Wisconsin- Madison. He grew up as a Missionary Kid in Liberia and came to the US at 16, to Little Rock. Fascinating guy.
After studying the figure for days and carefully and repeatedly counting the volumes, I think I've found all 67. There's no way that I could have independently thought of or visualized the correct compound, though.
Gad, I'm impressed. Excellent evidence that IQ is not that useful until it is combined with other abilities, such as creativity, proportionality, or in your case, diligence in seeking the truth. When I get into another IQ vs EQ vs vague "leadership" or "disciplined habits" discussion, you are likely to be a prime example.
My mind goes to theory (because SHORTCUT!), reasoning that 24 x 3 = 72, so that is the upper bound, but where did the 5 spaces go? If you believe empirically that it's 67, don't make yourself crazy with that. I am reminded of the joke about economists, when they see something working in practice, hurry back to their labs to see if it works in theory.
"I am reminded of the joke about economists, when they see something working in practice, hurry back to their labs to see if it works in theory."
In theory, there is no difference between theory and practice, but in practice there is.
Grouping the volumes by symmetry makes them easier to count. Let's start with the volumes visible from outside of the compound, using the picture in this blog post.
The top and bottom of the red cube each have a cross-shaped figure, composed by the blue and yellow cubes, jutting out. That's 4 volumes each. Double that since there's one on the top and one on the bottom. Cumulative count: 8
The other four faces of the red cube each have 3 blue volumes and 3 yellow jutting out of them. (3+3)*4 = 24 such volumes. Cumulative count: 8+24 = 32
Each of the 8 corners of the red cube is in its own volume. Cumulative count: 32+8 = 40
Then there are volumes in the middle of each of the 8 edges of the top and bottom faces of the red cube. Cumulative count: 40+8 = 48
Now for the harder part: internal volumes.
There's one volume each in the crosses on the top and bottom faces, where the blue and yellow wedges intersect. Cumulative count: 48+2 = 50
There are similar internal volumes in the blue/yellow wedges jutting out of the four other faces. Cumulative count: 50+4 = 54
Then four more where the edges of a blue or yellow cube contact the four edges which join the top face of the cube to its bottom face. Cumulative count: 54+4 = 58
The hardest to see are the volumes formed under the top cross or above the bottom cross, where the blue cube slices down into the red cube while bounded by a face of the yellow cube, or vice versa. There are four of those each for the top and bottom faces. Cumulative count: 58+8 = 66
Finally, the central volume, which I don't have a word to describe the shape of. It looks kind of like a clumsily sliced potato. Cumulative count: 66+1 = 67. That's all of them!
Mind you, counting the volumes with the figure right in front of me is much easier than solving the problem, which would have required intuiting the correct figure and then visualizing, drawing, or creating a model of it, and doubly so since I knew what target my count was supposed to hit.
I don't understand the reasoning of 24 x 3 = 72. However, if the idea is that there are 72 points of contact, I think that would result in 73 volumes, not 72. 73 is 6 more than 67. Maybe one volume goes 'missing' per face of one of the cubes because the planes which form the faces of the cubes don't extend infinitely? I don't see how that would work, but the number 6 points me in that direction.
As for IQ vs EQ debates, I think the high-IQ thing is to avoid them altogether. I'm no good example of disciplined habits, pudgy and without a university degree I am, and I don't think I've ever led anything of much importance either.
Also, I noticed last night that Chris Langan used the three-cube compound as the logo of his Mega Foundation. Answer leakage? He knew exactly what he was doing. Here's one version of it: https://scontent-atl3-1.xx.fbcdn.net/v/t39.30808-6/309239918_159307213394120_1372723559625400130_n.jpg?_nc_cat=103&ccb=1-7&_nc_sid=09cbfe&_nc_ohc=iqUG67QrFzEAX8vumsN&_nc_ht=scontent-atl3-1.xx&oh=00_AT_wjHSd3469cSRipeQ1B2xERlhUtPWw0cYELNbVZl7h4Q&oe=634F9BD2
Anyone out there have the answers for the Hoeflin Power Test? For some reason one of the questions popped into my mind today even tho I took the test (and the Mega) way back in 98. Specifically the question about drawing white marbles out of the container and the probability that all 10 marbles in the container are white. I honestly cannot see how my answer (51%) is wrong, but years ago a retired math professor told me the answer was in the 7% range which seems impossible
Check with Ganzir, above. He sent me some things, but I don't know that he wanted it distributed widely. He seemed a very reasonable young man when I corresponded with him.
If you can't trace him back by clicking, I have an old email for him.
Hello, I was cleaning out my e-mail inbox and noticed that I got an e-mail about the comment above. I don't believe Beartooth99 ever contacted me.
Are you still at joseph.j.hayes@outlook.com
He never took it any further with me, either.
Yes, that is still my primary e-mail address.
Post a Comment